Theoretical Model and Quantitative Assessment of Scientific Thinking and Reasoning
科学思维的理论模型与量化评估
A3. 科学思维模型新框架的构建
在学习探究的过程中,DCRs和MCRs都是知识生成过程中的重要基石。因此,知识的生成过程可以理解为一个整合DCRs 和 MCRs 而构建经过实验验证并在机制上得到合理解释的因果认知的过程。这个过程包括很多方面,因为它通常涉及具有多个变量的场景、背景以及DCRs和MCRs之间的协调过程,以形成更加一致和全面的因果理解。我们将这种思维和知识形成的过程称为基于数据协变和机制解释的因果思维框架(DMCR) ,该框架的建立基于前文所述工作的整合提升。由于DMCR过程在DCRs和MCRs之间进行整合协调,因此可以将其视为一个双路径过程,用于对涉及因果决策和知识形成涉及的推理进行操作建模。从这个角度来看,DMCR 框架与 Klahr 科学发现的双重搜索模型 (SDDS) 框架和Kuhn的理论证据协调模型具有共鸣。然而, DMCR 框架有其进步的特点,尤其是因果关系和因果思维的结构和功能过程是明确的且可进行操作性定义的。此外,科学思维被认为是在知识发展过程中对各种类型关系进行直接描述和建立的过程,这将在以下内容中进行详细讨论。
综合考虑所有的组成成分,形成了如图2所示的多变量因果关系的网络示意图,以及因果决策和知识生成的相关推理过程。该图说明了科学知识、科学探究、因果关系和科学思维之间的关系。在DMCR框架的表述中,将科学思维的概念进行概括性定义,它涵盖了支持因果思维、探究学习和知识形成的所有功能和过程。
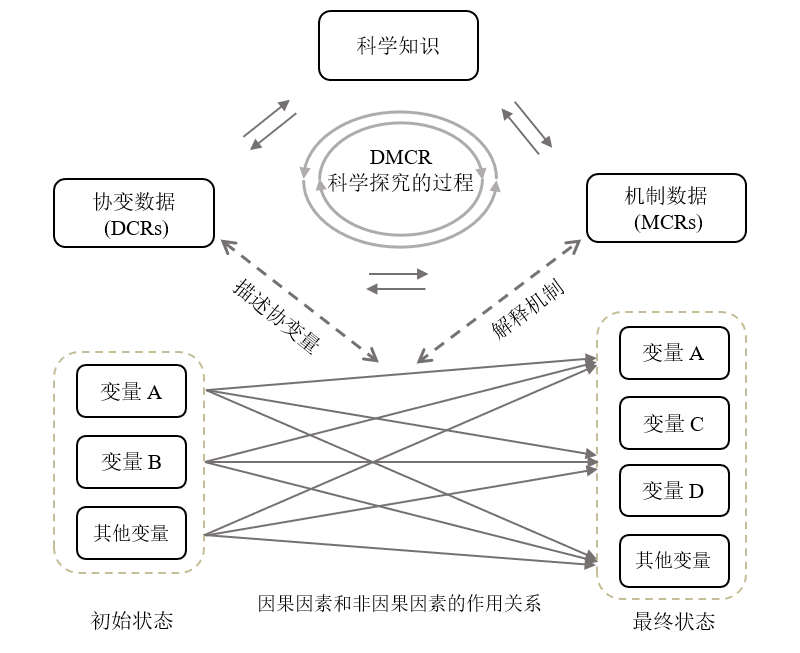
图2. DMCR科学思维的框架示意图,用来描述因果决策和知识的生成。设置的变量只是为了更形象的进行说明,并不代表任何具体实例。变量A表示初始状态和最终状态下都存在的特征,这些特征可能已经发生改变。变量B只存在于初始状态,而变量C和D仅在最终状态下出现。其他变量包括可能的受控、忽略或隐藏(未知)的变量。连接初始状态和最终状态变量的实线箭头表示可能的已知和未知变量之间的时间演化和场景交互,虚线箭头表示生成MCRs和DCRs的认知过程。
由于因果思维在科学探究和知识发展过程中起着至关重要的作用,因此该框架尤其注重其结构和过程的描述,如图2中的因果网络图所示。因果网络图表示一般时间顺序的因果事件,这些因果事件用初始状态、最终状态以及连接初始和最终状态的过程来进行描述。初始状态包含构成事件可能的因果和非因果因素的变量,而最终状态包含表示因果和非因果过程结果的变量。连接初始状态和最终状态的过程动态的描述了可能的因果和非因果动力学的条件及它们之间的作用机理。在图2所示的因果网络图中,初始状态的变量可以是因果的和非因果的,而最终状态的变量也可以是因果的和非因果的。过程中通常还涉及受控变量、未知或隐藏的其他变量。此外,由于测量条件的限制和外界环境的影响,描述初始状态和最终状态的变量集并不一定相同。
从初始到最终状态,可以分析描述在受控条件下的状态和收集发生变化的数据来识别和筛选DCRs。在这里,DCRs基于数据进行确认,描述从初态到终态的协变关系。然而,DCRs没有描述连接始末状态的机制过程。这些过程可以解释变量如何以及为什么可能发生协变,通过MCRs用因果机制进行描述和说明。使用如图2所示的因果关系模型,可以将理论和假设视为基于机制的解释。这是因为它们从机制上解释了连接相关变量的因果关系的结构和时间演变网络,可以通过实验观察并根据DCRs进行定量描述。完整的因果理论是由变量及其关系所形成的复合网络中的DCRs和MCRs作为支撑进行综合描述的,这被称为基于数据协变和机制解释的因果思维 (DMCRs),并通过因果思维过程来协调和重组 DCRs 和 MCRs。DMCRs代表充分发展的因果关系,构成特定内容领域中理论或已建立科学知识的基础。对于跨越多个知识领域的交叉概念和理论,它们通常建立为多领域 DMCRs 的集成网络。
例如,引力的经典理论涉及多个变量,包括两个有质量的物体,两个物体之间的距离,以及观察到的两个物体之间相互作用力的结果。三个变量之间的协变关系可以通过实验确定为 DCRs 并抽象形成数学关系,F=Gm_1 m_2/r^2, 以及对该方程机的机制解释 (MCR),即质量之间存在引力相互作用从而形成可观察到的力。总之,DCR 和 MCR 构成了经典引力理论的完整描述和解释框架。
对于科学知识,现有的大多数理论和假设都可以分解为相关变量之间的因果关系网络。一个成熟的理论将包括因果机制(MCRs)来解释协变关系(DCRs)的本质。以引力为例,该机制假设质量之间的引力相互作用导致引力的存在。然而,它充其量仍是一种基于观察的假设推断,其实际更深层次的机制仍未被理解。从哲学的角度来看,观察者可能永远无法理解或达到最终机制。
值得注意的是,在大多数情况下,DCRs是由初始状态和最终状态之间的协变变化确定的,而 MCRs 解释了将系统从初始状态转换为最终状态的机制过程。然而,在某些情况下,DCRs也可以是用来描述连接初始状态和最终状态的过程的特征定量分布。类似地,MCRs 也可以是用于确定初始和最终状态变量的基础机制。当特定领域的因果网络需要从根本上重构或扩展到其他网络时,会考虑这些附加属性,这部分内容超出了本文讨论的范畴。在这里,我们重点讨论的是DCRs和MCRs在特定知识领域的已建立因果网络中的主要功能。
图2中的多元因果网络也类似于贝叶斯网络的结构,该网络通常用于确定因果属性的概率特征。在定量因果决策中,贝叶斯概率在得出基于证据的结论中起着核心作用。因此,对多元因果网络和贝叶斯概率的理解和推理被列为评估科学思维的关键技能,本文稍后将对此进行详细讨论。
在以下内容中,将定义一些支持DCR和MCR推理路径的基本过程和元素。这些共同构成了构建科学思维和知识发展的 DMCR 框架模型的理论基础。这种更精细的细节对于创建一个评估框架并对相关的评估设计提供指导是至关重要的。