Theoretical Model and Quantitative Assessment of Scientific Thinking and Reasoning
科学思维的理论模型与量化评估
V.iSTAR测评工具的有效性和可靠性
iSTAR测评工具是历经十多年,通过广泛的定性定量研究逐渐发展起来的,其开发和验证也反应了一个逐渐完善科学思维工具和建模框架的过程。此处讨论的最新版本是2018年完成的稳定版本,可以通过附录中提供的线上系统使用。附录中的表A1还提供了题项级别的描述性统计数据。以下部分将重点介绍建立iSTAR测试的基本评估属性和有效性。
A. iSTAR的测评特点以及与LCTSR的比较
在本节中,将介绍不同人群iSTAR的描述性统计数据,以建立评估结果的基线。因为LCTSR是使用最广泛的科学思维评估工具,拥有庞大的用户群和数据库,因此将结果与LCTSR的测量值进行比较,以作为当前文献中现有结果的参考。同时,两者之间的比较也将有助于解释两种测评之间的异同。
如上一节所述,iSTAR包含3个通用技能维度,每个维度都包含不同复杂程度的多个子技能。比较来看,LCTSR则包含6个有限的技能维度。除了物质守恒维度,其他的LCTSR技能都可以对应到iSTAR维度上。因为物理守恒维度对初中及其以上水平的学生来说过于容易,所以该维度并未包含在iSTAR中 [37]。技能维度和相应的问题如表3所示。
表 3. iSTAR和LCTSR中技能维度和问题的对照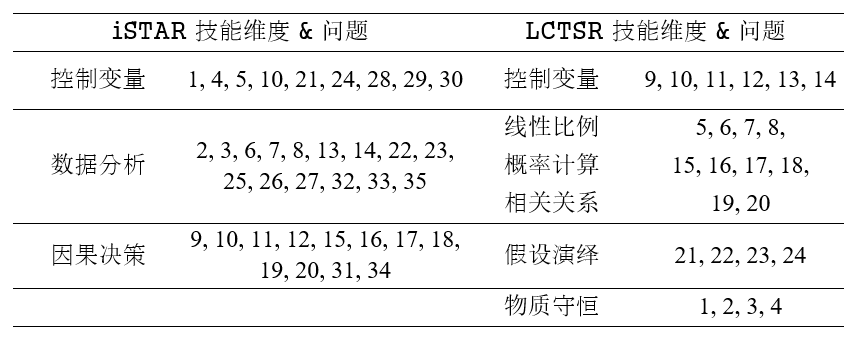
为了比较iSTAR和LCTSR的基线评估特征,对来自中西部郊区高中的高中生以及来自中西部综合性大学的大学生和研究生进行了随机A-B测试。其中,参与调查的大学生是正在上第一学期大学物理入门课程的新生,研究生是物理学专业博士二年级的学生。在高中和大学的测试中,学生们被随机分配iSTAR或LCTSR试卷(每个人只做一份)。研究生则采用了不同的测试流程,每个学生在同一周的两个不同时间都分别测试了iSTAR和 LCTSR,每个学生的两次测试顺序是随机的。iSTAR和LCTSR的平均得分见表4。
表 4. 随机A-B测试中iSTAR和LCTSR总分的比较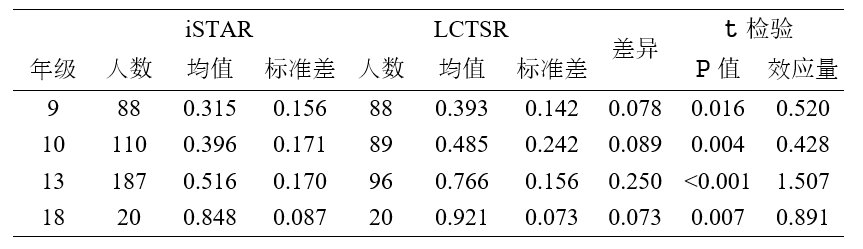
结果表明,所有年级学生的LCTSR分数始终高于iSTAR分数,说明iSTAR比 LCTSR难度更高。iSTAR解决了在测试大学生群体时LCTSR的天花板效应问题[37]。从结果可以看到,一年级大学生的差异最大,这可能是该年龄段技能发展和人群差异(即从高中进入大学的筛选过程)的结果。同时,研究生水平的较小差异可能是由于两个测试都具有的天花板效应。从不同年级平均分可以发现,iSTAR测量的技能开始在大学和研究生阶段得到更多发展,而 LCTSR 测试的技能似乎主要在高中到大学早期阶段得到发展。
为了比较同一类学生人群在两种测试上的表现,表4和图12分别列出和绘制了大学生的分数分布。结果表明iSTAR分数以50%左右为中心,接近正态分布。同时,LCTSR分数以80%左右为中心,分布偏高,天花板效应明显。
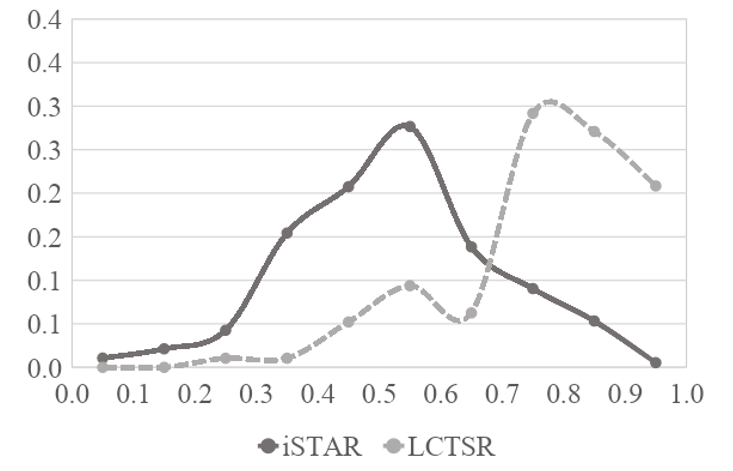
图 12. 大学生在iSTAR和LCTSR上的分数分布
对于同一组大学生,本研究对他们在iSTAR和LCTSR上的各个维度的得分进行了比较,如图13所示。结果表明,在三个常见维度上,LCTSR的维度得分显着高于 iSTAR(p<0.001 )。对于LCTSR,守恒维度的分数接近90%,这证实了这个维度对于大学生来说非常简单。在三个共同维度上,iSTAR呈现了难度从COV→DA→CDM维度的持续增加,这个结果验证了设计的预期,即控制变量是用于设置协变的基础,数据分析用于中间处理和分析,因果决策用于思维的整合。相比之下,LCTSR中因果决策维度问题的难度也是该测试题目中最高,平均分数为60%;然而,控制变量和数据分析维度的问题似乎对大学生来说比较容易,平均分数接近80%。尤其是数据分析与控制变量维度的问题处于相似水平,表明LCTSR缺乏对一些高级数据分析技能的测量。
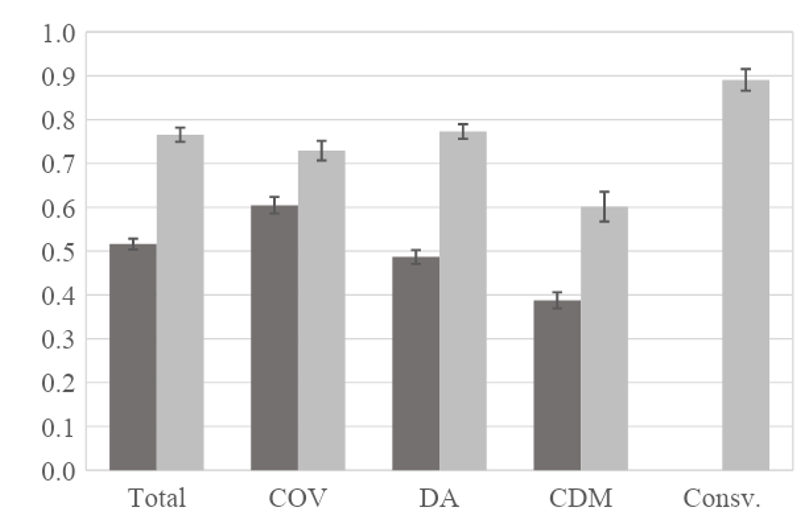
图 13. 大学生在iSTAR和LCTSR上的维度分数
通过对描述性统计的总结和比较,可以看出iSTAR的评估特点更适合大学生。学生在三个技能维度上的表现也呈现出了预期的难度等级进阶,这些进阶始终遵循前面讨论的数据协变与因果机制思维(DMCR)模型的预期设计。下一节将对iSTAR评估工具的有效性和可靠性作进一步的分析。