Theoretical Model and Quantitative Assessment of Scientific Thinking and Reasoning
科学思维的理论模型与量化评估
附件:iSTAR 测试的统计评估
1. 访问 iSTAR 测试
iSTAR 测试可以通过 https://istartest.com/home 上的在线测试系统访问和使用。有关使用测试的查询,请联系通讯作者获取更多信息。
2. 统计分析结果
表A1提供了iSTAR 试题的描述性统计数据,包括经典测量理论定义的试题难度(正确答案的分数)、试题区分度(高 30% 和低 30% 学生之间的分数差异)和单个试题的分数与测试总分之间的点二列相关(试题与总分的相关性)。计算结果与Rasch分析中用于评估结构效度的数据集相同。iSTAR的测试信度由Cronbach’s α评估,包含所有35个试题,结果为 0.737。其中两个试题(30 和 33)与测试总分相关性不显着。如果删除这两项,则Cronbach’s α变为 0.750。此类分析表明iSTAR 具有足够的可接受的信度。这两个试题保留在测试中,因为不同的人群可能会做出不同的反应,并且这两个试题是相关内容场景完整性所需的试题组的一部分。
表 A1. iSTAR的基本描述性统计(N=378)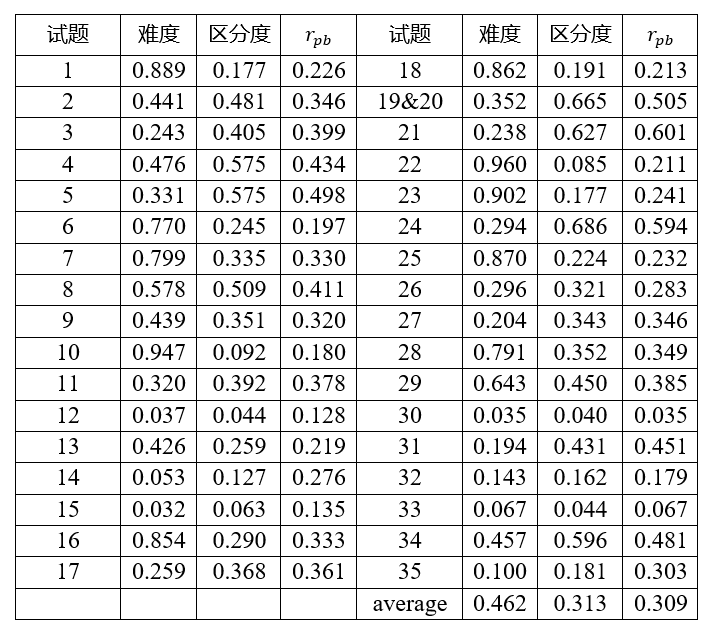
3. Rasch分析
为了调查这三个子技能是否代表学生科学思维和推理的不同维度,将三维模型与一维模型进行了,这里的一维模型假设数据背后只有一个潜在构造(即整体科学思维和推理)。两种模型的比较表明模型拟合参数有利于三维模型。似然比检验表明,与一维模型相比,三维模型在模型偏差方面显示出统计学上的显著改善(χ^2=65.793,df=5,p<0.001 )。
为证实上述模式拟合的结果,我们进一步探讨了三维模式的模型参数。在表A2中列出的加权和未加权均方残差 (MNSQ) 用于检查学生对 iSTAR 的反应在项目级别与Rasch模型的拟合程度。如表A2所示,iSTAR的所有项目,除了项目10、12和15,似乎都符合项目拟合标准(0.7<MNSQ<1.3)。对于第10、12和15项,虽然未加权MNSQ略微超出建议范围,但加权MNSQ很好地符合标准。因此,项目10、12和15没有从以下分析中删除。基于三维模型,在图 A1中绘制了怀特图。
表 A2. 由iSTAR 的 Rasch 模型估计的项目难度和拟合统计量(Infit 和 Outfit MNSQ)的度量。
请注意,平均项目难度被限制为零。参数估计旁边的星号表示它受到约束。
由于项目与总分相关性不显着,项目30和33未包括在该模型拟合分析中。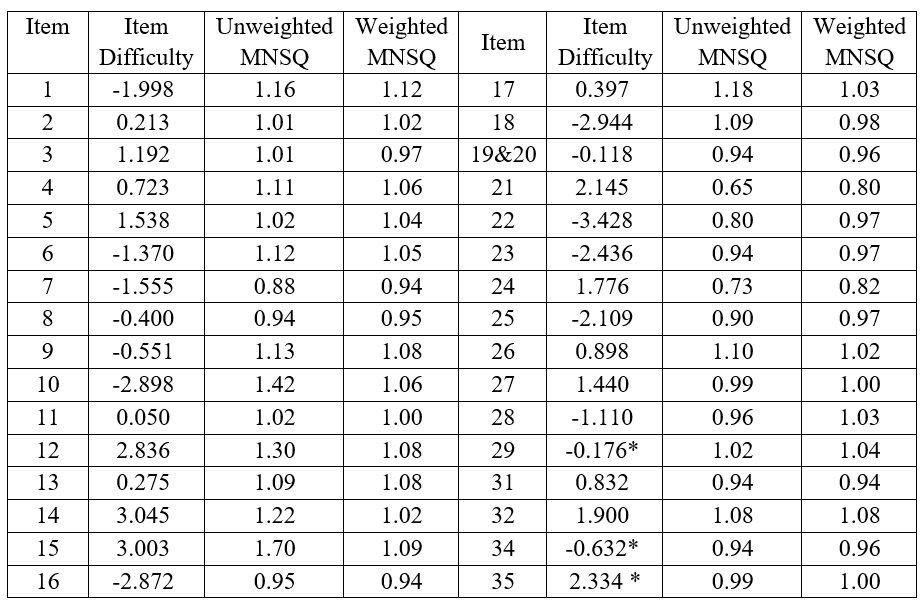
 图 A1 iSTAR怀特图
图 A1 iSTAR怀特图
表A2中的结果表明,项目难度的测量涵盖了从-3.428(容易)到 +3.045(困难)的足够广泛的范围。图A1中显示的怀特图为项目在三个技能组中的难度分布提供了进一步的细节。怀特图在相同的logit量表上显示单个学生的能力测量和单个项目的难度测量,以便在项目难度和学生表现之间进行清晰对应。iSTAR 数据使用三维 Rasch模型进行分析,该模型衡量学生的三个技能集,包括控制变量 (COV)、数据分析 (DA) 和因果决策 (CDM)。如图 A1 所示,项目难度广泛分布于三个技能维度,很好地涵盖了不同技能。对学生能力的测量也显示出在所有三个技能维度上理想的近正态分布,并且在能力量表上具有足够宽的跨度。三个技能维度上的能力分布中心也显示了预期的难度进阶,其中COV是最简单的(学生平均能力最高),DA是中级,CDM是最难的(学生平均能力最低)。总体而言,怀特图中显示的结果表明iSTAR 测试对三个技能维度的覆盖分布令人满意,并且提供的测量结果与设计的预期一致。